SymPy Demo 0: Welcome to SymPy and Jupyter Notebook

Demo by Karl Johan Måstrup Kristensen and Magnus Troen. Revised 24-10-24 by shsp.

Until now you have been working with what we call command line Python. Now we want to introduce you to a pair of new tools that will enable you to use Python as a proper CAS tool:

• SymPy

• Jupyter Notebook

SymPy is a Python package which permits the use of mathematical symbols, equation solving, and more. Jupyter Notebook is a tool for writing Python code and text in the same document for professional presentation.

SymPy will be your primary CAS tool in 01003 Mathematics 1a and 01004 Mathematics 1b, and the courses will be using Jupyter Notebook to present demos, examples, assignments, and projects. This demo is an introductory guide to SymPy’s basic functionalities as well as to using Jupyter Notebook.

Jupyter Notebook

Installation

Most likely you have already followed the DTU Python support’s installation guide (https://pythonsupport.dtu.dk/index.html) in other courses at DTU, which means that you already have all necessary tools installed. If not, then follow the installation guide now. A Jupyter Notebook file will have the file extension .ipynb. Note that our SymPy demos have been written in Jupyter Notebook, and you can download them as .ipynb via the download icon at the top of the page - try downloading this page now and follow the rest of the demo in your own editor.

Markdown

To bridge the gap between mathematical output from software and the mathematical reasoning associated with it, Jupyter Notebook allows for executable code and formatted text mixed in one document. Text formatting can be done using markdown syntax that allows for headlines, bold face, italic and more - see a full overview in the official markdown syntax guide. Also note that LaTex written with $...$ or $$...$$ will render in text such that a LaTex expression like $c=\sqrt{a^2+b^2}$ will render beautifully as: \(c=\sqrt{a^2+b^2}\). If you are new to LaTex, then we have added a bit more about LaTex last in this demo (under “Tips and Tricks” below).

We will not go further into markdown and LaTex syntax in this course, but we do encourage you to learn them and use them for creating professionally looking documents in all of your courses.

Code and text and key combinations

Note: The key combinations presented in these demos work in the code editor Visual Studio Code (VS Code), but most will also work in many other editors.

A Jupyter Notebook document is built of cells denoted by either python, containing code, or markdown, containing text. Execute a cell with the key combination Ctrl+Enter, or execute and jump to the next cell in one go by pressing Shift+Enter (if there is no next cell, then Jupyter Notebook will create one). Try this out by typing and running the following code in a new python cell in a Jupyter Notebook file:

print("Wow, this output is shown below the cell!")

Wow, this output is shown below the cell!

Note that not just python cells but also markdown cells must be “executed” - markdown will not be rendered if you simply leave the cell in editor mode without running it. Note that Shift+Enter lets you traverse through both python cells and markdown cells. The little blue marker to the left of the cells (in VS Code, but equivalently in other editors) indicates which cell is currently chosen.

Press Esc to leave editor mode in a cell without execution. Press Enter or double-click to reenter editor mode in a cell. If you have downloaded this demo, then try opening this cell and editing some text. When you are not in editor mode, then you can press m to convert a Python cell to a markdown cell, and y to convert a markdown cell to a Python cell.

You may now think: “Am I gonna have to use print() to show my results all the time?” No, Jupyter Notebook automatically prints the value of the last line in a python cell.

2+3+4+5+6*900

5414

Write several values separated by a comma, and these values will then be printed as a tuple (a list-like object that you may have come across in your previous work with Python).

2+3+4+5+6*900, 4**2, 5-6

(5414, 16, -1)

For the rest of this and future demos, if you are downloading the demo and viewing it in your editor (such as VS Code) then use Shift+Enter to execute Python cells and see the effects of the written code. If you read this demo on the website, then the outputs from python cells are shown by default.

See more shortkey combinations under “Tips and Tricks” last in this demo.

Import sympy and dtumathtools

From your programming courses at DTU as well as from our previous Theme exercises you will probably have seen packages being imported like this:

import cmath
import numpy as np

When a package is loaded, the commands, objects, and other contents that the package contains can now be accessed. With the above method of package import, one would have to write the package name (or the chosen prefix) apart from the command or object name each time a command or object from the package is to be used, for instance: cmath.polar() or np.array().

To allow for easier typing without the prefix, the package can instead be imported as follows, an import method which we will be using throughout the Mathematics 1 courses:

from sympy import *
init_printing()

The line from sympy import ... lets us access the functionality of the SymPy package without any prefix. You can specify the specific contents you need from the package by typing e.g. from sympy import sqrt, or you can load all contents by using the asterisk *, as we have done here.

The command init_printing() forces SymPy to print mathematical output from Python cells using nice LaTeX formatting:

pi**3 + 3 * pi**2 + pi

dtumathtools is a package specifically made for the Mathematics 1 courses by DTU. This package will make life a lot easier when plotting. You import dtumathtools in the same way as the sympy package.

from dtumathtools import *

Symbolic and Numerical Calculations

Python without SymPy stores its results and variable values numerically. This means that all numbers and variables are stored in the memory as a finite number of \(1\)’s and \(0\)’s at the core of it. The study of numerical mathematics and storage in digital electronics and computer science is left to other courses at DTU, but you should be aware that this can lead to unexpected and at the look of it “wrong” results.

As an example, we can of course all agree that

(1)\[\begin{equation} 0.3-(0.2+0.1) = 0. \end{equation}\]

But Python does not agree:

0.3-(0.2+0.1)

The output from Python is not exactly \(0\). Consequently, if we ask Python whether they are equal, using the logical operator ==, we get

0 == 0.3-(0.2+0.1)

False

Caution is therefore needed when checking numerical expressions for equality and in general when dealing with floating point numbers.

Many issues of this kind can be avoided by introducing SymPy to deal with the maths. Expressing our floating point numbers from before with fractions will allow SymPy to handle them in a more appropriate manner. To do that, insert your numerator or denominator into a SymPy command such as S(number), or Rational(numerator, denominator), or S('fraction'). SymPy will handle the maths better by keeping the number on rational form (exact form rather than approximate, numerical form).

Rational(3,10)-(S(2)/10 + S('1/10'))

If you wish to know more about how the S command handles the number behind the scenes, then search for singletons in the SymPy documentation.

Basic Mathematical Operators and Symbols

Python does not generally allow for symbolic mathematics. It allows you to assign values to symbols but not to assign expressions that contain variables or unknowns to symbols. Typing something like y=2*x+3 in Python will result in an error since x is undefined.

Symbols

This is where we see the strength of SymPy! With SymPy we can define our variable as a symbol as follows after which we can use the symbol freely in expressions:

# Mathematical symbol
x = symbols('x')

y=2*x+3
y

The symbols() command is the foundation for using Python as a CAS tool.

When solving equations, reducing expressions, and so on, all involved symbols must be defined, which can be done in one go:

x,y,z,l,p,t = symbols('x y z lambda phi theta')
x,y,z,l,p,t

Arithmetic Operations

As we have already seen, the basic operators \(+,-,*,/\) will work as you know them:

x+y, x-y, x*y, x/y

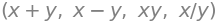
Other mathematical operations can be done using fitting commands from SymPy, such as square roots \(\sqrt{x}\) with sqrt(x) and the natural exponential function \(\mathrm e^x\) with exp(x). Note that sometimes Python uses different notation from what we are used to for certain operations. This is the case for powers \(x^y\), which you achieve in Python by typing x**y, and not by typing x^y as you would normally expect in other software.

sqrt(x), exp(x), x**y

Euler’s natural number is furthermore defined as E if one prefers that way of expressing exponential functions:

E**x

Symbols with Constraints

It will make your life with SymPy much easier if you define your symbols with as much information as possible. By default, SymPy will assume no constraints on your defined symbols, meaning your symbols will be assumed to be complex. So, if you know that your symbols are e.g. real numbers, or maybe you know that your symbol cannot be \(0\), then you can express it as follows:

# a is a real number
a = symbols('a', real = True)

# b can't be 0
b = symbols('b', nonzero = True)

# c is a real number and can't be 0
c = symbols('c', real = True, nonzero = True)

In some cases this will reduce the time SymPy needs to spend in later operations, and in other cases it will be the deciding factor in whether you even get an answer. Also, it lets SymPy reduce expressions further than it otherwise would.

Example on Symbols with and without Constraints

This example defines the expression \( \displaystyle\frac{\sqrt{x_1^2 + x_2^2}}{\sqrt{|x_1^2 + x_2^2|}},\quad x_1,x_2 \in \mathbb{R}. \)

First, let’s imagine that we “forget” to apply the known constraints. We just write:

# Symbols with no constraints
x1,x2 = symbols('x1,x2')

expression_x = sqrt(x1**2 + x2**2)/sqrt(abs(x1**2 + x2**2))

expression_x

Here, SymPy gives the full input as an output with no reduction at all.

But try tweaking this yourself in the following cell by adding the argument real = True as we saw above.

# Symbols with constraints
x1,x2 = symbols('x1,x2') # <- Change this line to add the contraint that x1 and x2 are real 

expression_y = sqrt(x1**2 + x2**2)/sqrt(abs(x1**2 + x2**2))

expression_y

The result should be that SymPy now is able to reduce the expression significantly. So, you will often want to provide SymPy with all the available information about symbols.

Equations

The equal sign = is in Python used to assign values to variables, and the double equal sign == is a logical operator that immediately evaluates a truth value. How then can we write out actual equations, now that equal signs are reserved for other purposes?

Defining Equations

You can do that using SymPy’s command Eq() in which you comma-separate the left-hand side and right-hand side. For example, the equation \(x^2=\frac13 y\) is written as Eq(x**2, S('1/3')*y). But remember to first define all involved unknowns as symbols.

x,y = symbols('x,y')
equation = Eq(x**2, y*S('1/3'))
equation

Now that your outputs are full equations and hence more complicated for python to generate, it could happen that the output is displayed without LaTex rendering. If so, then you have most likely forgotten to add or run init_printing() earlier in your document - but you can always just go back and run it.

Solving Equations

We gave a name to the equation above and called it equation. That allows us to retrieve it later where needed. We can e.g. try to solve this equation using a solver command in SymPy called solveset(equation, variable):

sols = solveset(equation, x)
sols

The output from solveset() will always be a mathematical set, in this case containing the several solutions to the equation. If any of these individual solutions are needed elsewhere, they can be accessed if you either first convert the solutions into a list, from which you then extract the solution you want,

list_of_solutions = list(sols)
list_of_solutions[0], list_of_solutions[1]

or you can loop through them all using e.g. a for loop:

for solution in sols:
    display(solution)

Infinitely many solutions: solveset() vs solve()

Other solver commands exist. The benefit of using solveset() is that SymPy gives you all solutions, which is very convenient when equations have infinitely many solutions. An example is the equation \(\sin(x) = 0\) which we solve as follows:

equation = Eq(sin(x), 0)
solveset(equation, x)

If we instead use SymPy’s older (and deprecated) solve() command to solve this equation, then we only get a few of the solutions:

solve(equation, x)

Of that reason we will mainly be using solveset() here in Mathematics 1a and 1b.

Constraints on Solutions

Sometimes only solutions within \(\mathbb{R}\) are wanted. solveset() by default provides all solutions in \(\mathbb{C}\), unless told otherwise. We can tell solveset() otherwise by adding a third argument to the command: solveset(equation, variable, domain), which defines the wanted domain from which solutions should be found.

As an example, the equation

x = symbols('x')
equation = Eq(exp(x), 1)
equation

has infinitely many solutions when \(x\in \mathbb{C}\),

solveset(equation, x)

but it only has a single solution when \(x\in\mathbb{R}\),

solveset(equation, x, S.Reals)

Common domains can be stated in SymPy as follows:

• S.Reals

• S.Complexes

• Interval(0, 1)

Mathematical Functions

Using a Standard Python Function

From your Python programming course at DTU you should already be aware of the following way to define a Python function:

# Standard Python function
def f(x):
    return x**2

x = symbols('x')
f(x)

The above Python function example defines the mathematical function \(f(x)=x^2,\) and you can now compute function values by typing f(2) and f(10) and the like. This type of Python function is able to handle SymPy objects, however it can pose problems when we do deeper mathematical functional work, such as differentiation.

Using Substitutions

As an alternative we can choose to define mathematical functions by simply assigning the expressions to variables.

# Mathematical function
fx = x**2

x = symbols('x')
fx

We now cannot do fx(2) to find function values, but for that purpose we can use .subs(variable, value) to substitute in a value for \(x\):

# Substituting x = 2
fx.subs(x, 2)

Dictionaries

.subs() can also handle dictionaries if we wish to insert multiple values. Dictionaries is a datatype in Python with the form

{x: 2, y: 2}

or

dict(x = 2, y = 2).

As an example, consider the following where we insert values for two variables:

# Function with two variables
fxy = x*y

x,y = symbols('x,y')

# Inserting x=1, y=2
fxy.subs({x: 1, y: 2}), fxy.subs(dict(x = 1, y = 2))

Mathematical functions defined in this manner can be differentiated with diff(function, variable, order). For example, in the following code line the first computation differentiates with respect to \(x\), the second differentiates to \(x\) twice (a second-order derivative), and in the second code line we perform partial differentiation of a function of two variables, first with respect to y, then to x:

diff(fx, x, 1), diff(fx, x, 2)

diff(fxy, y,1), diff(fxy,x,1)

Complex numbers

In SymPy, the imaginary unit \(i\) is defined as I.

I

Hence a complex number can be written as follows:

# Using S(1)/2, or equivalently S('1/2'), displays 1/2 as a fraction rather than as 0.5
z = S(1)/2 + I * sqrt(3)/2
z

We have a large arsenal of tools to work on the components of a complex number \(z\) at our disposal. For instance, we can tell SymPy to separate the real and imaginary parts using .as_real_imag():

z.as_real_imag()

Or we can find the modulus and argument of complex numbers using abs() and arg():

abs(z), arg(z)

Finding the complex conjugate is also easy using conjugate().

conjugate(z)

Simplifications and Forced Reductions

SymPy does not always display the most-reduced form of an expression. How much the output is reduced depends on the complexity of the expression and on what came before. For example, consider this small expression:

z/(5*z)

In cases like this, the command simplify() can be used to force the output down to the simplest possible (most reduced) version:

simplify(z/(5*z))

simplify() works generally, not just on complex expressions. So, when having trouble with an expression that will not reduce properly, try using simplify().

Switching between Complex Forms

Sometimes you will need to convert a complex number to its complex polar (exponential) form or to its rectangular form. The latter is achieved with .rewrite(sin) or .rewrite(cos).

# z is converted to polar form
z_exp = abs(z)*exp(arg(z)*I)
z_exp

# z is converted to rectangular form
z_rect = z_exp.rewrite(sin)
z_rect

In some cases, .rewrite(exp) can be used to go back to polar (exponential) form as in the following example:

# New rectangular form
t = symbols('t')
z1_rect = cos(pi/3 * t) + I*sin(pi/3 * t)
z1_rect

z1_rect.rewrite(exp)

Should this command not do the trick, then you must convert manually back to polar form as shown above.

Plots and dtumathtools, a brief look

As mentioned previously, the Python package dtumathools has been created specifically to make your Mathematics 1 experience at DTU easier. In this package you will find commands that you would otherwise only find equivalents of in specialized mathematical software like Maple (the software that was used in past versions of the course). dtumathools is mainly useful for easy plotting.

We will elaborate further on how to create more customized and advanced plots when it becomes relevant. For now we will just showcase a couple of simpler plots, with which you can check that you have the package installed correctly and working as expected.

Plotting

If you have not yet imported the package, then do it now.

from dtumathtools import *

Let’s define some symbols for the examples below.

# Defining symbols
x,y = symbols('x,y')

Plot function of one variable

dtuplot.plot plots functions of one variable. Note that you can set a vast amount of parameters to customize your plot:

func = 3*x**2
dtuplot.plot(func, xlim = [-5,10], ylim = [0,100], xlabel = 'x', ylabel = '$3x^2$' )

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f940b5e8460>

Plot equations

dtuplot.plot_implicit plots equations and inequalities:

# Implicit plot
eq = Eq((x - 1)**2 + (y+1)**2, 10)
dtuplot.plot_implicit(eq, (x,-5, 5), (y,-5, 5), aspect="equal")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f940b395610>

Plot parametric expressions

dtuplot.plot_parametric plots parametric representations in two dimensions:

# Parametric plot
vector_func = Matrix([x*cos(x), sin(x)])
dtuplot.plot_parametric(*vector_func, (x,0,2*pi))

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f940b5ef1c0>

For more, keep an eye out for the upcoming demos in future weeks. The dtumathtools package is homemade at DTU and thus does not have public official documentation - but we will go deeper into the use of the package as plots become more relevant, in particular in Mathematics 1b.

Tips and Tricks

Documentation

The material shown in this demo is only a small subset of what SymPy can do. We recommend that you make yourself familiar with the documentation, as it will be able to answer questions that we had not thought about when writing these demos. The documentation will expand your knowledge of and skills in the use of SymPy a lot.

The documentation can be found here:

• https://docs.sympy.org/latest/reference/index.html.

Note that you can get info directly from Python about any particular command or object by simply appending a question mark ? after the command or object name. See below, but note that when you run these code lines, then a large text with info from the documentation will appear:

Eq?

diff?

Using Software at the Math 1a Exam

The Math 1a exam in December will contain a part where electronic aid is allowed. We recommend that you train yourself in the use of SymPy such that you become an expert user of SymPy for this part of the exam. But remember that you will not have access to the internet at the exam. To be safe we thus recommend that you download the SymPy documentation to your computer from the following Github link before the exam so that you can look up syntaxes, command names, objects etc. that you would usually just have googled.

• sympy/sympy

Look for PDF or HTML when you download the documentation, as the other links on the Github page are for downloading the source-code for the package itself. When downloading as HTML, you can browse the downloaded docs the same way you can browse the SymPy-docs website.

Markdown and Mathematical Expressions with LaTex

If you are new to LaTex, then take a look through this section.

The markdown cells in Jupyter Notebook are capable of displaying mathematical expression with the so-called LaTeX syntax, which is how we have presented maths throughout this text and how we will continue to present it in future demos. LaTex can be written in a couple of ways, but to get you started we would like to present you with two methods.

In-line vs own-line LaTex

Inline math environments are created by typing $expression$ within text in a markdown cell. Use this to make rich text lines, such as: Let $x\in\mathbb{R}$, and let $P_2: \mathbb{R}\rightarrow\mathbb{R}$ denote an arbitrary quadratic polynomial., which will display as the following text line:

Let \(x\in\mathbb{R}\), and let \(P_2: \mathbb{R}\rightarrow\mathbb{R}\) denote an arbitrary quadratic polynomial.

For bigger expressions deserving of their own line, $$expression$$ is used. This will center and display the expression with more space than inline equations. Writing $$\lambda = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$$ as an example will render as follows:

\[ \lambda = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \]

You can raise to a superscript or lower to a subscript by writing $$x^2 \quad \text{and} \quad x_2$$:

\[x^2\quad \text{and}\quad x_2\]

Extra spacing and text within the LaTex expression were added here as well.

Dedicated Environments for larger Expressions

When creating larger portions of formatted mathematics, such as matrices, use a dedicated LaTex environment with $\begin{environment} ... \end{environment}$. The following matrix is written as $$\begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix}$$:

\[\begin{split} \begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix} \end{split}\]

Note how \\ separates rows while & separates columns. These features are also used in the following environment written as $$\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=10\\ \end{aligned}$$ used to write out an equation system neatly, where the & ensures alignment of the equation lines:

\[\begin{split}\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=10\\ \end{aligned}\end{split}\]

As you can see, LaTex is a different language separate from Python/SymPy that uses its own commands, which wrap around their input with curly brackets. LaTex is rich in functionality, encompassing a vast amount of commands and built-in environments, and you can use it to display basically anything. We recommend that you search on the internet for more examples of LaTex syntax that you can use in your documents on a daily basis. You do not need much to create rich mathematical assignments and reports.

Convert SymPy Output to LaTex

It can be quite tedious to type out in LaTex syntax an output that you got from SymPy, especially when dealing with larger outputs. Luckily, SymPy has the command print_latex() that converts SymPy expressions to LaTex code:

a,b,c,lamda = symbols('a:c, lambda')
expr = Eq(lamda, (-b+sqrt(b**2-4*a*c))/(2*a))
print_latex(expr)

\lambda = \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}

Then you can copy this output and paste it directly into a math environment, which in this case would yield:

\[ \lambda = \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a} \]

Keyboard shortcuts in VS Code

Make yourself familiar with VS Code’s built-in shortkeys and key combinations to make your work much easier. A few were mentioned in the beginning of this demo, and Microsoft has collected many more for VS Code in these cheatsheets:

• Windows og Linux

• macOS

If you are using another editor than VS Code, then it surely has similarly useful shortkeys that you should familiarise yourself with.

In case the vast overviews in the above links seem overwhelming, just remember this shortkey combination, depending on your operating system:

Windows or Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

This causes a search menu to pop up in VS Code. Here you can roughly type in what you are trying to do. Some useful search terms are:

• insert cell below or insert cell above

• create notebook

• change cell to code or change cell to markdown.

Try it below. Click on the code cell, bring up the search menu with the above shortkey combination, and then change the cell back and forth between code and markdown types.

equation = Eq(x**2 - 2 * x + 1, 0)
equation

When the desired action appears, you can select it with the arrow keys and press Enter.

If this action has a keyboard shortcut, it will be displayed on the right-hand side, and if not (or you should find the existing one inadequate) you can click on the gear icon on the right side and create your own keyboard shortcut.

Create new Jupyter Notebook

Open the search menu with:

Windows or Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

Search for and choose “Create: New Jupyter Notebook”. This creates a blank Notebook.

The new Notebook is saved and named with:

Windows eller Linux	macOS
Ctrl+S	CMD+S

Create new Cells

Hover your cursor between a cell and the next cell or between it and the previous cell and you will see an option appear for choosing between a cell for “Code” or “Markdown”. It will be created right there between the two cells. Have no cells been created yet, then these options will be permanently visible.

Alternatively you can use

Windows eller Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

and search for and choose “Notebook: insert”. Here you will be able to see all possibilities for inserting new cells.

Order of Execution

From your work with .py files (python script files) og command line programming you are used to the code being read top down. In Jupyter Notebook this is not the case.

Sure, within an individual Python cell, code will be executed top down (from the first code line to the bottom code line in that order), but different cells will be executed in the order in which you run them. If a variable is defined in a cell, then it applies to the entire Notebook when that cell is run no matter where the cell is located in the document; meaning this variable applies also to cells further up in the document.

Try as an example to execute the following four Python cells in the shown order:

# Cell 1
a = 1

# Cell 2
a = 5

# Cell 3
a = 2

# Cell 4
a + 2

Then try to execute only cell 2 and then cell 4. The result of the calculation in cell 4 clearly depends on which definition of \(a\) that was run latest. If you define a variable multiple times in your document, then the definition that applies will be the one that was run last, regardless of where you write it.

Thus, if you suddenly experience odd results, then it could be because some variables that you are using already are defined elsewhere, and maybe you have been clicking around and run them out of order. This is very common when working dynamically in a document. So, it might now and then be necessary to rerun your cells in the correct order - or to restart your Python kernel, or maybe to define your symbols anew with e.g. symbols(), such as for each new problem in an assignment, which will cleanse them from previously stored content.