SymPy Demo 1: Matrix Algebra and Determinants

Demo by Jakob Lemvig, Christian Mikkelstrup, Hans Henrik Hermansen, Karl Johan Måstrup Kristiansen, and Magnus Troen. Revised 18-10-24 by shsp.

from sympy import *
init_printing()

Matrices and Systems of Equations

A Linear System with one Solution

We wish to solve the system

\[\begin{split}\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=9.\\ \end{aligned}\end{split}\]

This can be done in many different ways - let’s go through some methods in the follow subsections.

Method 0 - Define all Equations

It is an option to simply define all equations and get SymPy to solve them.

x1,x2,x3 = symbols('x1:4')
eq1 = Eq(-x2 + x3, 2)
eq2 = Eq(2*x1 + 4*x2 - 2*x3, 2)
eq3 = Eq(3*x1 + 4*x2 + x3, 9)
eq1, eq2, eq3

SymPy solves systems of linear equations with the linsolve() command.

linsolve((eq1,eq2,eq3), (x1,x2,x3))

We see that the system has exactly one solution:

\[\begin{split} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \\ 1\end{bmatrix}. \end{split}\]

Method 1 - Convert the System to Matrix form

Another approach to solving an equation system is when you have the coefficient matrix \(\mathbf A\) and the right-hand side vector \(\mathbf b\) of the system. Since we already have the equations defined above, the linear_eq_to_matrix() command can be used to extract this matrix and vector.

A,b = linear_eq_to_matrix([eq1,eq2,eq3],[x1,x2,x3])
A,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right], \ \left[\begin{matrix}2\\2\\9\end{matrix}\right]\right)\end{split}\]

Defining Matrices

Often you will have to manually define your matrix, though. This is done with the Matrix() command:

A = Matrix([
    [0,-1,1],
    [2,4,-2],
    [3,4,1]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right]\end{split}\]

Your input in this command must be each row as a list with a comma between the lists. Note how you must add a wrapping [...] around all these lists. Be careful not to mistakenly assume that your lists will be merged as columns in the matrix you generate - always check your output carefully after a code line.

An alternative way to input the elements into the Matrix() command is the following where you fill out the indicated number of rows and columns row-vice from left to right:

Matrix(3,2,[1,2,3,4,5,6])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\3 & 4\\5 & 6\end{matrix}\right]\end{split}\]

Defining Vectors

A vector is defined using the same command. Here you just leave out the wrapping [...] and input only one list. This list is then interpreted as a column vector:

b = Matrix([2,2,9])
A,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right], \ \left[\begin{matrix}2\\2\\9\end{matrix}\right]\right)\end{split}\]

In summary, we define matrices by inputting a list of lists where each inner list designates a row, while we define column vectors by inputting one list and nothing more:

• Matrix([[a,b,c],[d,e,f],[g,h,i]]) produces \(\displaystyle{\begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix}}.\)

• Matrix([a,b,c]) produces \(\displaystyle{\begin{bmatrix} a\\b\\c \end{bmatrix}}.\)

Solving Using Matrix Form

It is a typical mistake to forget the wrapping [...] around the lists of rows when defining a matrix. Python will then output an error, which you can format as follows if you wish:

# Example on a wrongly defined matrix
try:
    Matrix([1,2,3], [4,5,6], [7,8,9])
except:
    print("The [] around the rows is missing")

The [] around the rows is missing

The linsolve() command from Method 0 above is also capable of taking matrices as input: linsolve((A,b)).

When a coefficient matrix \(\mathbf A\) and a right-hand side vector \(\mathbf b\) are defined, linsolve() can be used to find the solution:

linsolve((A,b))

Method 2 - Gauss Elimination and Reduced Row-Echelon Form

Gauss-Jordan solve

When we have defined the coefficient matrix and the right-hand side of the system, then SymPy can also solve the system using Gauss-Jordan elimination with .gauss_jordan_solve(right-hand side).

A.gauss_jordan_solve(b)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}4\\-1\\1\end{matrix}\right], \ \left[\begin{matrix}\end{matrix}\right]\right)\end{split}\]

This method is generally really nice from a user’s point of view. However, it will result in an error if the system has no solutions.

A2 = Matrix(2,2, [1,2,0,0])
b_no_solution = Matrix([1,2])

try:
    A2.gauss_jordan_solve(b_no_solution)
except Exception as e:
    print(e)

Linear system has no solution

Reduced Row-Echelon Form

We can alternatively construct the augmented matrix as we would do by hand:

\[ \mathbf{T} = [\mathbf{A} | \mathbf{b}]. \]

If \(\mathbf A\) and \(\mathbf b\) are defined, then a neat command called .hstack() can merge them together side by side into a new matrix:

T = Matrix.hstack(A,b)
T

\[\begin{split}\displaystyle \left[\begin{matrix}0 & -1 & 1 & 2\\2 & 4 & -2 & 2\\3 & 4 & 1 & 9\end{matrix}\right]\end{split}\]

From here we can find the Reduced Row-Echelon Form with .rref().

T.rref(pivots = False)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right]\end{split}\]

This again gives us the solution \(x_1 = 4\), \(x_2 =-1\), and \(x_3 =1 \).

pivots = False just lets SymPy know that we do not care about in which columns the pivots are located. Without this argument we get the following output which conveys a bit more information if needed:

T.rref()

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right], \ \left( 0, \ 1, \ 2\right)\right)\end{split}\]

Method 3 - Simulated Manual Computation

SymPy also allows us to perform Gauss-Jordan elimination step by step, meaning by performing elementary row operations as one would do manually. You might want to do this when you do not want to immediately solve your system or to immediately reduce your matrix fully because you need insight into the intermediate steps. Using SymPy to do row operations in this manner is what we call simulated manual computational work.

To reach the reduced row-echelon form, we resolve the columns one by one. The first column is resolved by first switching around row 1 and row 2, then multiplying the new row 1 by \(1/2\), and lastly adding \(-3\) times row 1 to row 3. Note the SymPy syntax for these three types of row operations in the following:

T1 = T.elementary_row_op('n<->m', 0, 1)
T2 = T1.elementary_row_op('n->kn', 0, S(1)/2)
T3 = T2.elementary_row_op('n->n+km',2,-3,0)
T1,T2,T3

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 4 & -2 & 2\\0 & -1 & 1 & 2\\3 & 4 & 1 & 9\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & -1 & 1 & 2\\3 & 4 & 1 & 9\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & -1 & 1 & 2\\0 & -2 & 4 & 6\end{matrix}\right]\right)\end{split}\]

Now the last two columns are handled as follows:

T4 = T3.elementary_row_op('n->kn',1,-1)
T5 = T4.elementary_row_op('n->n+km',2,2,1)
T6 = T5.elementary_row_op('n->n+km',0,-2,1)
T4,T5,T6

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 2 & -1 & 1\\0 & 1 & -1 & -2\\0 & -2 & 4 & 6\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & 1 & -1 & -2\\0 & 0 & 2 & 2\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 1 & 5\\0 & 1 & -1 & -2\\0 & 0 & 2 & 2\end{matrix}\right]\right)\end{split}\]

T7 = T6.elementary_row_op('n->kn',2,S(1)/2)
T8 = T7.elementary_row_op('n->n+km',0,-1,2)
T9 = T8.elementary_row_op('n->n+km',1,1,2)
T7,T8,T9

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 1 & 5\\0 & 1 & -1 & -2\\0 & 0 & 1 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & -1 & -2\\0 & 0 & 1 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right]\right)\end{split}\]

From the reduced row-echelon form that we have reached, we read the same solution as from the other methods.

This method, strenuous as it is, can be necessary when solving systems that contain variable or unknown coefficients, since SymPy will not catch “exceptions” and “special-cases”. To be more clear, if your matrix contains an unknown and you at some point want to carry out a row operation that divides by an expression containing this unknown, then the value of the unknown that would lead to a division by zero - hence the value that we will have to treat as a special-case afterwards - will be ignored by SymPy.

A Linear System with Multiple Solutions

We now wish to solve the inhomogenous system, for which the coefficient matrix is given by

A = Matrix([[1,3,2,4,5],[2,6,4,3,5],[3,8,6,7,6],[4,14,8,10,22]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 3 & 2 & 4 & 5\\2 & 6 & 4 & 3 & 5\\3 & 8 & 6 & 7 & 6\\4 & 14 & 8 & 10 & 22\end{matrix}\right]\end{split}\]

and the right-hand side by

b = Matrix([9,3,5,32])
b

\[\begin{split}\displaystyle \left[\begin{matrix}9\\3\\5\\32\end{matrix}\right]\end{split}\]

Method 1 - Solving directly in SymPy

We have already seen several different methods for solving an equation system, methods that of course also work for inhomogeneous systems. Let’s use some of them:

A.gauss_jordan_solve(b)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- 2 \tau_{0} + 11 \tau_{1} - 24\\7 - 4 \tau_{1}\\\tau_{0}\\3 - \tau_{1}\\\tau_{1}\end{matrix}\right], \ \left[\begin{matrix}\tau_{0}\\\tau_{1}\end{matrix}\right]\right)\end{split}\]

linsolve((A,b))

In this example the solutions will contain free parameters (because there are infinitely many solutions). The output from SymPy shows the symbols \(\tau_0\) and \(\tau_1\), which are these free parameters. They in general fulfill \(\tau_0, \tau_1 \in \mathbb{F}\).

The SymPy outputs are not easy to read, and we prefer to present our solutions in standard parametric form. So, we write out the SymPy output using Latex for nice presentation:

\[\begin{split}\mathbf x= \begin{bmatrix}-24\\7\\0\\3\\0\end{bmatrix} +\tau_0\begin{bmatrix}-2\\0\\1\\0\\0\end{bmatrix}+\tau_1\begin{bmatrix}11\\-4\\0\\-1\\1\end{bmatrix}\quad , \tau_0,\tau_1\in\mathbb F.\end{split}\]

Note that SymPy uses zero indexing, so a list of free parameters as here will be numerated starting from \(0\). It is recommended that you always write out e.g. in Latex syntax your SymPy outputs into text form when presenting your results to a reader.

Method 2 - Solving via rref()

First we construct the augmented matrix by:

T = A.row_join(b)
T

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 3 & 2 & 4 & 5 & 9\\2 & 6 & 4 & 3 & 5 & 3\\3 & 8 & 6 & 7 & 6 & 5\\4 & 14 & 8 & 10 & 22 & 32\end{matrix}\right]\end{split}\]

Then we find the reduced row-echelon form

T.rref()

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 2 & 0 & -11 & -24\\0 & 1 & 0 & 0 & 4 & 7\\0 & 0 & 0 & 1 & 1 & 3\\0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right], \ \left( 0, \ 1, \ 3\right)\right)\end{split}\]

From this form we can easily read the solution to be:

\[\begin{split} \begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5 \end{bmatrix}= \begin{bmatrix}-24\\7\\0\\3\\0 \end{bmatrix}+ \tau_0\begin{bmatrix}-2\\0\\1\\0\\0 \end{bmatrix}+\tau_1\begin{bmatrix}11\\-4\\0\\-1\\1\end{bmatrix} \quad , \tau_0,\tau_1\in\mathbb F. \end{split}\]

We omitted the argument pivots=False from the command this time in order to clearly be able to see which columns that contain pivots. There are no pivots in columns 3 and 5, hence the variables \(x_3\) and \(x_5\) will be our free paramters \(\tau_0\) and \(\tau_1\) in this example.

Check

Let’s check that the number of free parameters is correct. We have found two in the above.

The number of variables is \(n=5\), hence the number of free parameters should be equal to \(n-\rho(\mathbf A)\), where \(\rho\) is the rank of the matrix.

A.rank()

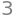
5-A.rank()

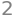
As expected.

Matrix Algebra

Fundamentals

We will use the follow matrices for the examples in this section:

A = Matrix([[2,1],[3,0],[7,11]])
B = Matrix([[1,1],[9,3],[-7,-1]])
C = Matrix([[2,1,3],[-6,5,8]])
A,B,C

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 1\\3 & 0\\7 & 11\end{matrix}\right], \ \left[\begin{matrix}1 & 1\\9 & 3\\-7 & -1\end{matrix}\right], \ \left[\begin{matrix}2 & 1 & 3\\-6 & 5 & 8\end{matrix}\right]\right)\end{split}\]

We can multiply matrix \(\mathbf A\) with a scalar like this:

k = symbols('k')
k*A

\[\begin{split}\displaystyle \left[\begin{matrix}2 k & k\\3 k & 0\\7 k & 11 k\end{matrix}\right]\end{split}\]

Since \(\mathbf A\) and \(\mathbf B\) have the same dimensions, \(\mathbb{R}^{3\times 2}\), the matrix sum \(\mathbf A+\mathbf B\) is defined.

A+B

\[\begin{split}\displaystyle \left[\begin{matrix}3 & 2\\12 & 3\\0 & 10\end{matrix}\right]\end{split}\]

We can also compute linear combinations, for example \(3\mathbf A-5\mathbf B\):

3*A-5*B

\[\begin{split}\displaystyle \left[\begin{matrix}1 & -2\\-36 & -15\\56 & 38\end{matrix}\right]\end{split}\]

Since the number of columns in \(\mathbf A\) matches the number of rows in \(\mathbf C\), we can compute the matrix product \(\mathbf A \cdot \mathbf C\).

A*C

\[\begin{split}\displaystyle \left[\begin{matrix}-2 & 7 & 14\\6 & 3 & 9\\-52 & 62 & 109\end{matrix}\right]\end{split}\]

Note that the matrix product generally doesn’t commute, so in general \(\mathbf A\mathbf C \neq \mathbf C\mathbf A\), as the following makes clear:

display(A*C, C*A)

\[\begin{split}\displaystyle \left[\begin{matrix}-2 & 7 & 14\\6 & 3 & 9\\-52 & 62 & 109\end{matrix}\right]\end{split}\]

\[\begin{split}\displaystyle \left[\begin{matrix}28 & 35\\59 & 82\end{matrix}\right]\end{split}\]

The transposed matrix can be found with several different commands:

A.T, A.transpose(), transpose(A)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right], \ \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right], \ \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right]\right)\end{split}\]

The rank of a matrix is easily computed with:

A.rank()

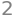
If a matrix is invertible, then the inverse is found with .inv():

M = Matrix([[2,0,1],[1,2,0],[-2,1,4]])

M*M.inv()

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]\end{split}\]

Indexing Matrices

We can access the elements in a matrix by considering the matrix as a 2D array. The command M[n,m], where M is a matrix, will give us the element located in row \(n\) and column \(m\). Now it is of particular importance to remember that Python uses zero-indexing.

We will be considering the matrix:

M = Matrix([[2,0,1],[1,2,0],[-2,1,4]])
M

\[\begin{split}\displaystyle \left[\begin{matrix}2 & 0 & 1\\1 & 2 & 0\\-2 & 1 & 4\end{matrix}\right]\end{split}\]

The element in row 3 and column 3 is accessed as follows:

M[2,2]

To access an entire column, use the M.col() command. The following will give you column no. 2:

M.col(1)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\2\\1\end{matrix}\right]\end{split}\]

For rows the equivalent M.rows() is used.

M.row(0)

\[\displaystyle \left[\begin{matrix}2 & 0 & 1\end{matrix}\right]\]

We can be even more sophisticated in our handling of the contents of a matrix. If we want to remove the first row and the last column, then we just tell SymPy that we want it to return only the last two rows and the first two columns. We do that using slices as follows:

M[1:, :2]

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\-2 & 1\end{matrix}\right]\end{split}\]

See more about slicing in Python by searching the internet.

SymPy can be used to produce a submatrix. We mathematically would use the notation \(\mathbf A(i; j )\), which denotes a new matrix identical to the old matrix but without row \(i\) and column \(j\) (see the course textbook for more). The method for that is M.minorMatrix(i,j).

M.minorMatrix(0,-1)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\-2 & 1\end{matrix}\right]\end{split}\]

Determinants

Consider the following matrix:

\[\begin{split}\mathbf A = \begin{bmatrix} 0 & 2 & 3 & 4 \\ 2 & 0 & 4 & 3 \\ 3 & 4 & 0 & 2 \\ 4 & 3 & 2 & 0\end{bmatrix}.\end{split}\]

To find the determinant, SymPy has a neat built-in command:

A = Matrix([[0,2,3,4],[2,0,4,3],[3,4,0,2],[4,3,2,0]])
A.det()

Or equivalently:

det(A)

The determinant of a submatrix \(\det(\mathbf M(i;j))\) can of course be computed by first retrieving the submatrix and then finding the determinant of it, so det(M.minorMatrix(i,j)). But a direct command added directly to the original matrix also exists: M.minor(i,j).

det(M.minorMatrix(0,-1)), M.minor(0,-1)

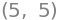
Applications of Determinants

Existence of Inverses

Consider the matrix

\[\begin{split} \mathbf A = \left[\begin{matrix}1 & 2 & 3\\2 & 4 & 1\\3 & a & 7\end{matrix}\right]. \end{split}\]

We wish to determine \(a \in \mathbb{R}\) such that \(\mathbf A\) is invertible. According to the course textbook, \(\mathbf A\) is invertible if and only if \(\operatorname{det}(\mathbf A) \neq 0\). We therefore wish to solve

\[ \operatorname{det}(\mathbf A) = 0 \]

for \(a\). This will give us all instances of \(a\), for which \(\mathbf A\) is not invertible. That is done as follows:

a = symbols('a', real = True)
A = Matrix([[1,2,3],[2,4,1],[3,a,7]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 4 & 1\\3 & a & 7\end{matrix}\right]\end{split}\]

solveset(Eq(det(A), 0), a, S.Reals)

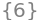
Hence \(\mathbf A\) is invertible for \(a \in \mathbb{R}\setminus\{6\}\).

Linear (In)dependence

Consider the following four vectors in \(\mathbb{C}^4\):

\[\begin{split} \mathbf v_1 = \left[\begin{matrix}1 + i\\3\\0\\7 i\end{matrix}\right], \ \mathbf v_2 = \left[\begin{matrix}2\\4 - i\\2 i\\8 - i\end{matrix}\right], \ \mathbf v_3 = \left[\begin{matrix}3 + i\\7 - i\\2 i\\8 + 6 i\end{matrix}\right], \ \mathbf v_4 = \left[\begin{matrix}3\\-1 - i\\7 i\\0\end{matrix}\right]. \end{split}\]

v1 = Matrix([1+I, 3, 0 , 7*I])
v2 = Matrix([2, 4-I, 2*I, 8-I])
v3 = Matrix([3+I, 7-I, 2*I, 8+6*I])
v4 = Matrix([3,-1-I, 7*I, 0])

We wish to determine whether \(\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4\) are linearly independent. Firstly, let

\[ \mathbf A = [\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4]. \]

A = Matrix.hstack(v1,v2,v3,v4)
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 + i & 2 & 3 + i & 3\\3 & 4 - i & 7 - i & -1 - i\\0 & 2 i & 2 i & 7 i\\7 i & 8 - i & 8 + 6 i & 0\end{matrix}\right]\end{split}\]

We now find the determinant of this matrix:

det(A)

Since \(\det(\mathbf A) = 0\), we can conclude that the vectors \(\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4\) are linearly dependent (see the relevant theorem that states this in the course textbook).

Let us now just focus on \(\mathbf v_1,\mathbf v_2,\mathbf v_4\). Is this set of just three of the vectors linearly independent? Since \(\mathbf B = [\mathbf v_1,\mathbf v_2,\mathbf v_4] \in \mathbb{C}^{4 \times 3}\) is not a square matrix, we cannot find the determinant and thus we cannot use the method above. Instead we will look at their linear combination and investigate whether any non-zero coefficients exist such that this linear combination can equal zero (see the course textbook for more).

Let \(c_1,c_2,c_3 \in \mathbb{C}\) be arbitrary scalars, and assume

\[ c_1 \mathbf v_1 + c_2 \mathbf v_2 + c_3 \mathbf v_4 = 0. \]

This corresponds to an equation system whose coefficient matrix is the three vectors merged as columns. We solve this system:

cs = symbols('c:3')
B = Matrix.hstack(v1,v2,v4)
linsolve((B,zeros(4,1)), cs)

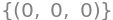
The only solution is \(c_1 = c_2 = c_3 = 0\). Hence \(\mathbf v_1,\mathbf v_2,\mathbf v_4\) are linearly independent.

Tips and Tricks on Constructing Matrices

Some prefer to write matrices into SymPy as follows:

Matrix(3,3,[1,2,3,4,5,6,7,8,9])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{matrix}\right]\end{split}\]

Here, the (3,3) indicates the dimensions, and the rows in the matrix can then be written by simply listing all elements as a single list [1,2,3,...], instead of creating one list per row.

Identity matrices are easily created in SymPy using eye(dimension):

eye(3), eye(3,2)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0\\0 & 1\\0 & 0\end{matrix}\right]\right)\end{split}\]

Diagonal matrices can be defined by Matrix.diag(elements):

Matrix.diag([1,2,3,4,5])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0\\0 & 2 & 0 & 0 & 0\\0 & 0 & 3 & 0 & 0\\0 & 0 & 0 & 4 & 0\\0 & 0 & 0 & 0 & 5\end{matrix}\right]\end{split}\]

Full 0-matrices or 1-matrices can be created with zeros(m, n) and ones(m, n):

zeros(2), ones(3,2)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & 0\\0 & 0\end{matrix}\right], \ \left[\begin{matrix}1 & 1\\1 & 1\\1 & 1\end{matrix}\right]\right)\end{split}\]

ones(m,n) can also be used to create a matrix where all elements are the same:

k = 7
k * ones(3,2)

\[\begin{split}\displaystyle \left[\begin{matrix}7 & 7\\7 & 7\\7 & 7\end{matrix}\right]\end{split}\]

More advanced matrix constructions can be achieved with Matrix(m, n, lambda i,j: expression), which ends with an expression that describes what should happen with each element. For example:

Matrix(3,2, lambda i,j: 3*i + j)

\[\begin{split}\displaystyle \left[\begin{matrix}0 & 1\\3 & 4\\6 & 7\end{matrix}\right]\end{split}\]

We can for example create an identity matrix like this:

Matrix(3,3, lambda i,j: 1 if i == j else 0)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]\end{split}\]