SymPy Demo 6: Differential Equations and Systems hereof

Demo by Karl Johan Måstrup Kristiansen and Magnus Troen. Revised 29-10-24 by shsp.

from sympy import *
init_printing()

1st-Order Linear Differential Equations

According to a theorem in the course textbook, a 1st-order linear differential equation in the form

\[ f'(t) = p(t)f(t) + q(t) \]

can be solved using the formula

\[f(t) = \mathrm e^{P(t)}\int \mathrm e^{-P(t)} q(t)\ \mathrm dt, \]

where \(P(t)\) is an antiderivative of \(p(t)\).

As an example, we are now for \(t\in\mathbb{R}\) given the following inhomogenous differential equation:

\[ f'(t) + 4\cdot f(t) = \mathrm e^{3t}. \]

We wish to find the general solution to this equation as well as a particular solution that fulfills the following initial-value condition:

\[f(1) = 5.\]

Solving Manually with SymPy Aid (Simulated Manually)

The General Solution

In order to use the above-mentioned formula, we first rewrite our differential equation to the required form:

\[ f'(t) = -4\cdot f(t) + \mathrm e^{3t}. \]

We define the components \(p(t) = -4\) and \(q(t)=\mathrm e^{3t}\) in SymPy:

t = symbols('t', real = True)

# Define p(t) and q(t)
pt = -4
qt = exp(3*t)

We now set up the integrand (the contents within the integral in the formula, so \(\mathrm e^{-P(t)} q(t)\)). For that we need a \(P(t)\), an antiderivative of \(p(t)\), which can be found by integrating \(p(t)\). SymPy has the neat command integrate() for that:

# Find an antiderivative P(t)
Pt = integrate(pt,t)

# Construct the integrand
integrand = simplify(exp(-Pt)*qt)
integrand

Note that SymPy does not add a constant to the result when integrating. The integrate() command finds an antiderivative, not the full indefinite integral. But when computing the integral from the formula as our next step, this constant is important, so we will have to manually add a \(c_1 \in \mathbb{F}\) ourselves:

c1 = symbols('c1')

# Determine f(t) using the formula
f_t = exp(Pt)*(integrate(integrand,t) + c1)
f_t

This is the general solution.

We could of course attempt to carry out all of the above in one code line, such as the following:

# Remove the comment from the following line to see if SymPy can run it:

# exp(integrate(pt,t))*(integrate(exp(-integrate(pt,t))*qt,t) + c1)

This might work this time, but SymPy can often run into trouble with integrations when the integrand becomes complicated. When that happens then we recommend that you split up your calculation as we have done in the above and find the components beforehand as well as find the integrand and simplify it as much as possible before doing the integration on it.

A Particular Solution from Initial-Value Condition

The general solution \(f(t)\) that we found in the above contains infinitely many solutions. This is due to the constant \(c_1\), which can take any value. Only one particular solution among them fulfills the given initial-value condition \(f(1) = 5.\)

We can find this particular solution by solving for the value of the constant \(c_1\) that let’s \(f(t)\) fulfill the condition:

# The initial condition
eq = Eq(f_t.subs(t,1), 5)

# Solve for c_1
c1_sp = solveset(eq, c1).args[0]
c1_sp

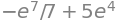
We insert this value of the constant into the general solution to find the wanted particular solution:

f_p = simplify(f_t.subs(c1, c1_sp))
f_p

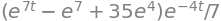
Let us do a check to confirm that \(f_{p}(t)\) indeed does fulfill the differential equation we were given to begin with, as well as a check to confirm that it indeed does fulfill the given initial-value condition:

simplify(diff(f_p,t) + 4*f_p) == qt

True

f_p.subs(t,1) == 5

True

Solving Directly with SymPy Commands

Symbolic Functions

As you know very well at this point, you cannot use and display an unknown variable or constant before defining it as a symbol using symbols('variable_name'). Similarly, you cannot handle and display an unknown function either unless you define it as a symbolic function using the command Function('function_name'):

t = symbols('t')
f = Function('f')

f(t) , diff(f(t),t) , f(t)+t**3+4

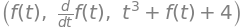
If more than one function is needed, then we will again use the symbols() command but with the extra argument cls=Function indicating that we are dealing with symbolic functions:

f,g,h = symbols('f g h', cls=Function)
f1, f2, f3, f4 = symbols('f1:5', cls=Function)

display([f(t),g(t),h(t)])
display([f1(t), f2(t), f3(t), f4(t)])

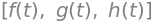
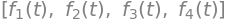
The General Solution using dsolve

With the function name defined symbolically, we can define and display our differential equation in its full form before solving it:

ode1 = Eq(diff(f(t),t) + 4*f(t), exp(3*t))
ode1

SymPy can solve this differential equation directly with the command dsolve():

sol = dsolve(ode1)
sol

Note how the output from dsolve() includes the function name, so it has the format: f(t)=expression. To retrieve only the expression so that you can continue working with it, you need to extract from this output the right-hand side:

sol.rhs

A Particular Solution using dsolve() with Initial-Value Conditions

To find the particular solution that fulfills the given initial-value condition \(f(1)=5\), we simply add the condition as an argument to dsolve():

dsolve(ode1, ics={f(1): 5})

As an alternative, dtumathtools has a wrapper for the differential equation that returns a dictionary instead:

from dtumathtools import *

dtutools.dsolve([ode1], ics = {f(1):5})

This is nice later on as it works with .subs(), making use of the solutions in other parts of the assignment easier.

Homogeneous Systems of 1st-Order Differential Equations

See the course textbook for the solution formulas for the different cases of homogeneous differential equation systems of order 1. We will be using one such solution formula in the following example.

As an example, we are now for \(t\in\mathbb{R}\) given the following system:

\[\begin{split} \begin{cases} f_1'(t) = 2f_1(t) - \frac{1}{2}f_2(t)\\ f_2'(t) = \frac{1}{3}f_1(t) + f_2(t). \end{cases} \end{split}\]

We see that the system is homogeneous (since there are no forcing functions involved). We wish to find the general solution to the system as well as the particular solution that fulfills the initial-value conditions \(f_1(0) = 1\) and \(f_2(0) = 0\).

Solving Manually with SymPy Aid (Simulated Manually)

The General Solution

The system can be written in matrix form as:

\[\begin{split} \begin{bmatrix} f_1'(t)\\ f_2'(t) \end{bmatrix} = \begin{bmatrix} 2 & -\frac{1}{2}\\ \frac{1}{3} & 1 \end{bmatrix} \begin{bmatrix} f_1(t)\\ f_2(t) \end{bmatrix}. \end{split}\]

According to a theorem in the course textbook the solution structure depends on the eigenvalues of the system’s matrix. So, let’s define the system’s matrix as \(\mathbf A\):

A = Matrix([[2,-S(1)/2],[S(1)/3, 1]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}2 & - \frac{1}{2}\\\frac{1}{3} & 1\end{matrix}\right]\end{split}\]

and compute its eigenvalues:

A.eigenvals()

The eigenvalues are real but not equal, so we will use a solution formula from the textbook where the solution has the following structure:

\[ \boldsymbol f(t) = c_1 \mathbf{v}_1 \mathrm e^{\lambda_1 t} + c_2 \mathbf{v}_2 \mathrm e^{\lambda_2 t}, \]

where \((\mathbf{v}_i, \lambda_i)\) for \(i = 1,2\) are pairs of eigenvectors and eigenvalues of the system’s matrix, and \(c_1,c_2\in \mathbb{F}\) are constants. Keep in mind that the solution, here written as \(\boldsymbol f(t)\), consists of two functions, \(\boldsymbol f(t)=(f_1(t),f_2(t))\).

We now need eigenvectors as well, so we use the command:

ev = A.eigenvects()
ev

\[\begin{split}\displaystyle \left[ \left( \frac{3}{2} - \frac{\sqrt{3}}{6}, \ 1, \ \left[ \left[\begin{matrix}\frac{3}{2} - \frac{\sqrt{3}}{2}\\1\end{matrix}\right]\right]\right), \ \left( \frac{\sqrt{3}}{6} + \frac{3}{2}, \ 1, \ \left[ \left[\begin{matrix}\frac{\sqrt{3}}{2} + \frac{3}{2}\\1\end{matrix}\right]\right]\right)\right]\end{split}\]

This gave us all necessary components to plug into the solution structure:

t = symbols('t', real = True)
c1,c2 = symbols('c1,c2')
sol_hom = c1* ev[0][2][0]*exp(ev[0][0]*t) + c2*ev[1][2][0]*exp(ev[1][0]*t)
sol_hom

\[\begin{split}\displaystyle \left[\begin{matrix}c_{1} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)} + c_{2} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right) e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}\\c_{1} e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)} + c_{2} e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}\end{matrix}\right]\end{split}\]

This is hence the general solution to the given homogeneous system. Note how this solution is expressed in vector form because the solution contains two functions. The top one (the first coordinate in the vector) is \(f_1(t)\), and the bottom one is \(f_2(t)\).

We can check that this is correct by confirming that

\[\begin{split} \begin{bmatrix}f_1'(t)\\f_2'(t)\end{bmatrix} - \mathbf{A}\begin{bmatrix} f_1(t)\\f_2(t)\end{bmatrix} = \mathbf{0}. \end{split}\]

simplify(diff(sol_hom, t) - A*sol_hom)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\0\end{matrix}\right]\end{split}\]

A Particular Solution from Initial-Value Condition

As before, the above general solution contains infinitely many solutions. We now wish to find a particular solution among them which fulfills the given initial conditions \(f_1(0)=1\) and \(f_2(0)=0\), meaning we wish to find values of \(c_1\) and \(c_2\) such that \(\begin{bmatrix}f_1(0)\\f_2(0)\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}.\)

A particular solution to this system will consist of two functions, \(f_1(t)\) and \(f_2(t)\), and each of the given conditions applies to just one of these functions. So, we will have to manually pluck each function out from the general solution in order to substitute in the conditions:

sol_sp = zeros(2,1)
sol_sp[0] = sol_hom[0].subs(t,0)
sol_sp[1] = sol_hom[1].subs(t,0)
b = Matrix([1,0])
sol_sp,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}c_{1} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) + c_{2} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right)\\c_{1} + c_{2}\end{matrix}\right], \ \left[\begin{matrix}1\\0\end{matrix}\right]\right)\end{split}\]

We have here substituted the value of \(t\) (which for both is \(t=0\)) into each of the functions, after which we defined the right-hand sides as a vector \(\mathbf b\).

We will now solve these two equations simultaneously. When solving multiple equations with solve(), all equations should be passed as homogeneous without the usual Eq(). Do not write:

\[ \verb|solve(Eq(sol_sp,b))| \]

but instead write:

\[ \verb|solve([sol_sp - b])| \]

cs = solve([sol_sp - b])
cs

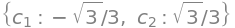
Another option is to write these equations in matrix form as well and then to use linssolve() on them:

B,b = linear_eq_to_matrix(sol_sp - b, [c1,c2])
display((B, b))
linsolve((B, b))

\[\begin{split}\displaystyle \left( \left[\begin{matrix}\frac{3}{2} - \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} + \frac{3}{2}\\1 & 1\end{matrix}\right], \ \left[\begin{matrix}1\\0\end{matrix}\right]\right)\end{split}\]

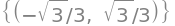
Regardless of the approach, we have now found the particular solution that fulfills the given initial-value condition to be (again remember that the first expression in the vector represents \(f_{1p}(t)\) and the second \(f_{2p}(t)\)):

sol_hom.subs(cs)

\[\begin{split}\displaystyle \left[\begin{matrix}- \frac{\sqrt{3} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)}}{3} + \frac{\sqrt{3} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right) e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}}{3}\\- \frac{\sqrt{3} e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)}}{3} + \frac{\sqrt{3} e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}}{3}\end{matrix}\right]\end{split}\]

Solving Directly with SymPy’s dsolve()

We once again define our differential equations using symbolic functions. Let’s define those first:

f1 = Function('f1')
f2 = Function('f2')

f = Matrix([f1(t),f2(t)])
f

\[\begin{split}\displaystyle \left[\begin{matrix}f_{1}{\left(t \right)}\\f_{2}{\left(t \right)}\end{matrix}\right]\end{split}\]

To define the system, do not use Eq()! Instead, write the system with everything on one side of the equal sign:

\[\begin{split} \begin{bmatrix} f_1'(t) \\ f_2'(t)\end{bmatrix} = \mathbf{A} \begin{bmatrix} f_1(t)\\ f_2(t) \end{bmatrix} \quad\Leftrightarrow\quad \begin{bmatrix} f_1'(t) \\ f_2'(t)\end{bmatrix} - \mathbf{A} \begin{bmatrix} f_1(t)\\ f_2(t)\end{bmatrix} =\mathbf 0 \quad\Leftrightarrow\quad \boldsymbol f'(t)-\mathbf A\cdot \boldsymbol f(t)=\mathbf 0, \end{split}\]

where \(\boldsymbol f'(t)\) simply means that all functions within \(\boldsymbol f\) are differentiated. Then define \(\boldsymbol f'(t)-\mathbf A\cdot \boldsymbol f(t)\) in SymPy. The system’s matrix \(\mathbf A\) was already defined as A above, so we now just do:

df = diff(f,t)

ode_sys = df - A * f
ode_sys

\[\begin{split}\displaystyle \left[\begin{matrix}- 2 f_{1}{\left(t \right)} + \frac{f_{2}{\left(t \right)}}{2} + \frac{d}{d t} f_{1}{\left(t \right)}\\- \frac{f_{1}{\left(t \right)}}{3} - f_{2}{\left(t \right)} + \frac{d}{d t} f_{2}{\left(t \right)}\end{matrix}\right]\end{split}\]

We are now ready to solve the system with a single SymPy command. As before we have two options: SymPy’s version and the dtumathtools version. The only difference is the type of output, since dsolve() returns a list of equations while dtutools.dsolve() returns a dictionary with each function paired with its respective right-hand side:

dtutools.dsolve(ode_sys, ics = {f1(0):1, f2(0):0})

dsolve(ode_sys, ics = {f1(0):1, f2(0):0})

We have now found the particular solution that fulfills the initial-value conditions. You can remove the ics argument to obtain the general solution instead.