Exercises – Short Day#
Exercise 1: From Degrees to Radians and vice versa#
In this exercise we wish to brush up on how angles measures in degrees can be converted to radians and vice versa.
Question a#
State the angles \(30, 60, 120, 135,\) and \(300\) degrees in radians.
Answer
\(\frac{\pi}{6}\), \(\frac{\pi}{3}\), \(\frac{2\pi}{3}\), \(\frac{3\pi}{4}\), \(\frac{5\pi}{3}\). In general, \(x\) degrees corresponds to \(x \pi / 180\) (radians).
Question b#
Sketch a unit circle in a \((x,y)\) coordinate system centred at the origin. Draw points on the cirle that correspond to each of the arc lengths
Which angle measures in degrees do they correspond to?
Answer
\(180\), \(60\), \(330\), \(330\), \(105\), \(90\), \(315\). In general, an arc length of \(x\) (radians) corresponds to \(180x/\pi\) degrees if \(x \in [0,2\pi[\). If \(x \not\in [0,2\pi[\), then we should first add a multiple of \(2\pi\) such that the result is located in the interval \([0,2\pi[\).
Exercise 2: Cosinus and Sinus Brush Up#
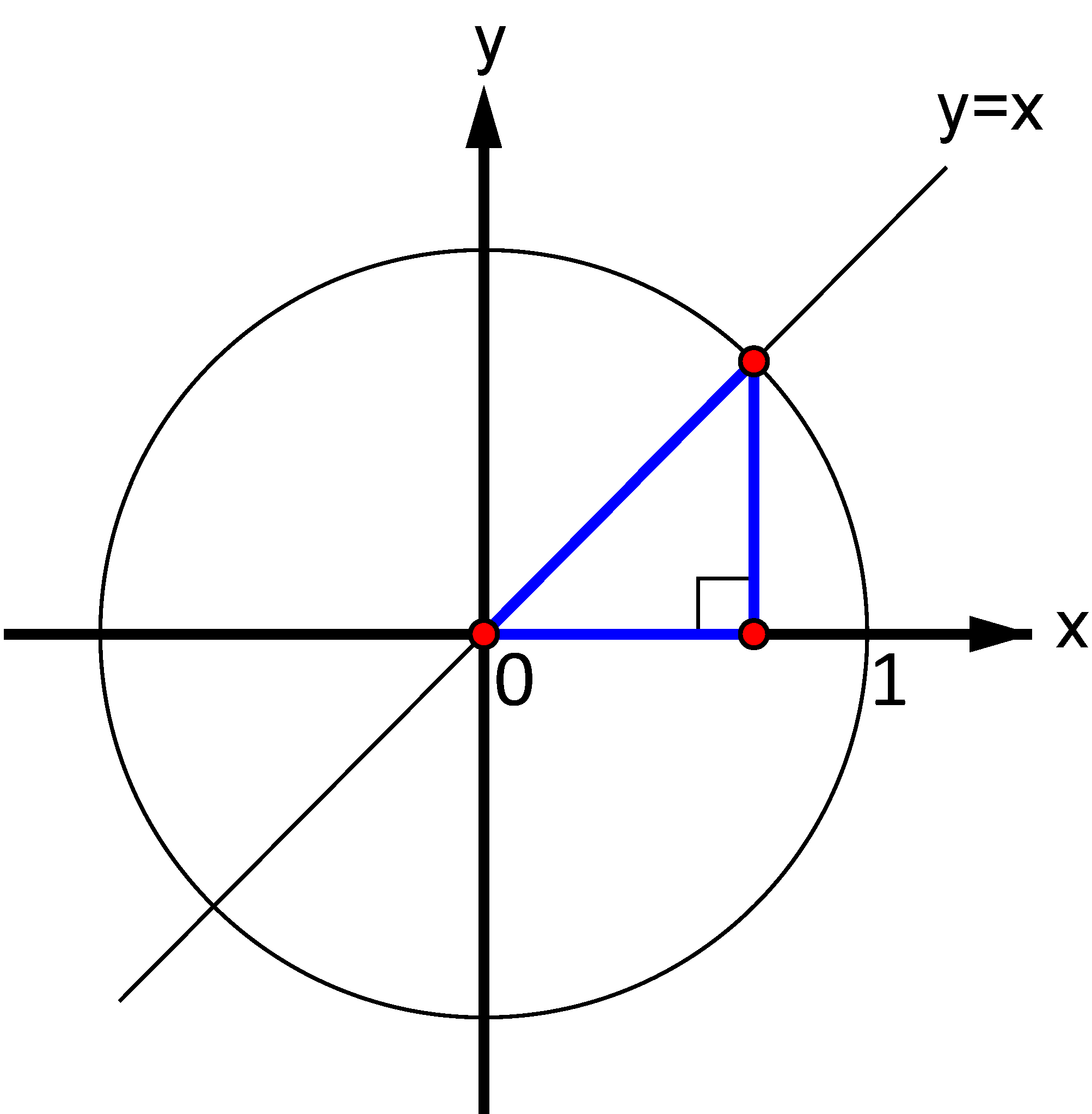
Question a#
Use the figure above (the blue triangle) for geometric determination of the exact values of \(\,\displaystyle{\cos\left(\frac{\pi}{4}\right)}\,\) and \(\,\displaystyle{\sin\left(\frac{\pi}{4}\right)}\,.\)
Hint
Remember that the Pythagorean Theorem implies \(\cos^2(x)+\sin^2(x)=1\) for all real numbers \(x\) - this is often called the “dummy rule”.
Answer
Both are \(\frac{\sqrt{2}}{2}\,. \)
Question b#
Determine via symmetry considerations the numbers
Answer
\((-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}),(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}),(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}), (-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}).\)
Question c#
We are informed that \(\,\displaystyle{\cos\left(\frac{\pi}{6}\right)}=\frac{\sqrt 3}{2}\,\) and \(\,\displaystyle{\sin\left(\frac{\pi}{6}\right)}=\frac{1}{2}\,.\) Draw the point
on a unit circle and find via symmetry considerations the numbers
Hint
Note: in Appendiks 1 in the textbook, found right after the last chapter, you can find a unit circle along with consine and sine values of several often-used and “nice-looking” angles.
Exercise 3: The Functions \(\mathrm{arccos}\), \(\mathrm{arcsin}\), and \(\mathrm{arctan}\)#
In this exercise we consider the inverse trigonometric functions \(\mathrm{arccos}\), \(\mathrm{arcsin}\), and \(\mathrm{arctan}\). If a brush-up is needed, or you’d like to view the graphs of these functions, have a look in Section 2.3 in the textbook (in particular the subsection “The Inverse Trigonometric Functions”).
Question a#
State the numbers corresponding to \(\,\displaystyle{\mathrm{arccos}\left(\frac{1}{2}\right),\,\mathrm{arcsin}\left(-\frac{\sqrt 3}{2}\right)},\) and \(\displaystyle{\mathrm{arctan}(-1)}\,.\)
Answer
\(\frac{1}{3} \, \pi\), \(-\frac{1}{3} \, \pi\), \(-\frac{1}{4} \, \pi\).
Question b#
Let \(x \in \mathbb{R}\) and \(y \in [-1,1]\) be real numbers. Let \(P\) be the logical proposition \(\mathrm{arccos}(y)=x\) and \(Q\) the logical proposition \(y=\cos(x)\). Show that \(P \Rightarrow Q\) is true whereas \(Q \Rightarrow P\) is not necessarily true.
Hint
Regarding \(P \Rightarrow Q\), what happens if one uses the \(\cos\) function on both sides of the equal sign in \(P\)?
Regarding \(Q \Rightarrow P\), can you find an \(x \in \mathbb{R}\) and a \(y \in [-1,1]\) such that \(Q\) is true while \(P\) isn’t?
Exercise 4: Cosinus and Sinus Brush Up, Part 2#
This exercise continues from Exercise 3.
Question a#
We are given the sets \(\,A=\left[\,0\,,\,2\pi\,\right]\,\) and \(\,B=\left[\,-\pi\,,\,\pi\,\right]\,.\)
Solve the equation \(\,\displaystyle{\cos(x)=\frac{1}{2}}\,\) within each of the sets \(\,A,\,B,\,\) and \(\,\Bbb R\,.\)
Hint
A solution to the equation can be state immedicately based on Question 3a, since there we found that \(\mathrm{arccos}(y)=x\) implies \(y=\cos(x).\) Now find all solutions within \(\mathbb{R}\) by first drawing a sketch of the graph of the \(\cos\) function.
Answer
Within \(A\) the solutions are \(\,\frac{\pi}{3}\,\) and \(\,\frac{5\pi}{3}\,.\)
Within \(B\) the solutions are \(\,\frac{-\pi}{3}\,\) and \(\,\frac{\pi}{3}\,.\)
Within \(\mathbb{R}\) the solutions are \(\,\frac{-\pi}{3}+p\cdot 2\pi\,\) and \(\,\frac{\pi}{3}+p\cdot 2\pi\,,\) where \(\,p \in \Bbb Z\,.\)
Question b#
Solve the equation \(\,\displaystyle{\sin(x)=-\frac{\sqrt 3}{2}}\,\) within each of the sets \(\,A,\,B\,\) and \(\,\Bbb R\,.\)
Answer
Within \(A\) the solutions are \(\,\frac{4\pi}{3}\,\) and \(\,\frac{5\pi}{3}\,.\)
Within \(B\) the solutions are \(\,\frac{-2\pi}{3}\,\) and \(\,-\frac{\pi}{3}\,.\)
Within \(\mathbb R\) the solutions are \(\,\frac{4\pi}{3}+p\cdot 2\pi\,\) and \(\,\frac{5\pi}{3}+p\cdot 2\pi\,,\) where \(\,p \in \Bbb Z\,.\)
Exercise 5: Polar Coordinates#
Question a#
We are given the numbers \(z_1=1+i\sqrt{3}\,\), \(z_2=-1+i\sqrt{3}\,\), \(z_3=-1-i\sqrt{3}\,\), and \(z_4=1-i\sqrt{3}\,\).
Draw \(z_1\), \(z_2\), \(z_3\), and \(z_4\) in the complex plane and state their rectangular coordinates.
Compute the moduli (also known as the absolute values) of \(z_1\), \(z_2\), \(z_3\), and \(z_4\). Conclude that the four numbers are located on a circle centred at \(0\). What is the radius of this circle?
Determine the principal arguments of \(z_1\), \(z_2\), \(z_3\), and \(z_4\) and state their polar coordinates.
Hint
For assistance with the calculation of modulus and principal argument, see Theorem 4.3.1 (and also Figure 4.5) in the textbook.
Hint
\(\mathrm{arctan}(\sqrt{3})=\pi/3\), since \(\tan(\pi/3)=\frac{\sin(\pi/3)}{\cos(\pi/3)}=\frac{\sqrt{3}/2}{1/2}=\sqrt{3}.\)
Answer
Partial answer:
\(z_1\): The rectangular coordinates of the number are \((1,\sqrt{3})\) while its polar coordinates are \((2,\pi/3)\).
\(z_2\): The rectangular coordinates of the number are \((-1,\sqrt{3})\) while its polar coordinates are \((2,2\pi/3)\).
\(z_3\): The rectangular coordinates of the number are \((-1,-\sqrt{3})\) while its polar coordinates are \((2,-2\pi/3)\).
\(z_4\): The rectangular coordinates of the number are \((1,-\sqrt{3})\) while its polar coordinates are \((2,-\pi/3)\).
Question b#
Someone is about to find the polar coordinates of the complex number \(\,-2+2i\,\,\). He/she chooses to use a pocket calculator. First the following is typed in:
which gives the output \(\,2\sqrt{2}\,\) as the absolute value. Then the following is typed in:
which gives the output \(\,\displaystyle{-\frac {\pi}4}\,.\)
This answer is wrong. Where is the error?
Question c#
Find absolute value and principal argument of the following complex number:
Answer
Absolute value is \(\frac{1}{3}\). Principal argument is \(\frac{2}{3} \, \pi\).
Question d#
We are given the following information about the moduli and arguments of three complex numbers \(z_1\), \(z_2\), and \(z_3\):
and
Note that we haven’t necessarily been given the principal argument of the numbers, just an argument.
Determine the principal argument of the numbers.
Find the rectangular form of the numbers.
Hint
The principal argument (or “the principal value of the argument”) of a complex number is the one argument that is located in the interval \(]-\pi,\pi].\) If the argument you have been given is not already within this interval then add a well-chosen multiple of \(2\pi\), such that the result is moved to the interval \(]-\pi,\pi].\) Read the beginning of Section 4.3 from the textbook for more information.
Hint
For finding the rectangular form, Equation (3.4) in the textbook may be of use.
Answer
The principal arguments are \(\pi\), \(-2\pi/3\), and \(-3\pi/4\).
The numbers in rectangular form are \(-4\), \(-1-i \, \sqrt{3}\), and \(-3 \, \sqrt{2} - i \, 3 \, \sqrt{2}\).
