Exercises – Short Day#
Exercise 1: Brush-Up on Recursion and Summation Notation#
We define a sequence of numbers \(c_0,c_1,c_2,\dots\) recursively as follows:
\(c_0=0\), \(c_1=1\), \(c_2=2\), and for \(n \ge 3\) we let \(c_n=c_{n-1}c_{n-2}+c_{n-3}.\)
Question a#
Which values do \(c_3,c_4,\) and \(c_5\) take?
Answer
\(c_3=c_2c_1+c_0=2\cdot 1+0=2.\)
\(c_4=c_3c_2+c_1=2\cdot 2+1=5.\)
\(c_5=c_4c_3+c_2=5\cdot 2+2=12.\)
Question b#
Which values does \(\sum_{k=0}^n c_k\) take for \(n=0,1,2,3,4,\) and \(5\)?
Hint
In place of the summation symbol, “dot” notation can also be used: \(\sum_{k=0}^n c_k=c_0+\cdots + c_n\).
Answer
\(\sum_{k=0}^0c_k=c_0=0.\)
\(\sum_{k=0}^1c_k=c_0+c_1=1.\)
\(\sum_{k=0}^2c_k=c_0+c_1+c_2=1+2=3.\)
\(\sum_{k=0}^3c_k=c_0+c_1+c_2+c_3=3+c_3=5.\)
\(\sum_{k=0}^4c_k=c_0+c_1+c_2+c_3+c_4=5+c_4=10.\)
\(\sum_{k=0}^5c_k=c_0+c_1+c_2+c_3+c_4+c_5=10+c_5=22.\)
Exercise 2: The Sum of Odd Numbers and Induction#
Question a#
Calculate for \(n=1,2,3,4\) the sum of the first \(n\) odd natural numbers. In other words, calculate the value of \(\sum_{k=1}^n (2k-1)\) for \(n \in \{1,2,3,4\}.\) Is there a pattern in the found values?
Now, find/guess a short expression for \(\sum_{k=1}^n (2k-1)\) that produces the right answer for \(n \in \{1,2,3,4\}\), and check that your guess also produces the right value of \(\sum_{k=1}^n (2k-1)\) for \(n=5.\)
Hint
The found values are always squares.
Answer
\(\sum_{k=1}^1 (2k-1) = 1\), \(\sum_{k=1}^2 (2k-1) = 4\), \(\sum_{k=1}^3 (2k-1) = 9\), and \(\sum_{k=1}^4 (2k-1) = 16\).
Based on the above it is reasonable to make the guess that \(\sum_{k=1}^n (2k-1)=n^2\) is true for all natural numbers \(n\). For \(n=5\), this guess fits as well: \(5^2=25\) and \(1+3+5+7+9=25\).
Question b#
Let \(P(n)\) be the logical proposition that \(\sum_{k=1}^n (2k-1)\) equals the short expression you provided in Question a. Now the goal is to show that \(P(n)\) is true for all natural numbers \(n\) (meaning, for all \(n \in \mathbb{N}=\mathbb{Z}_{\ge 1}\)).
Show that the base case of the induction holds true.
Hint
The base case is the proposition \(P(1)\). In other words, to show that the base case holds true, you must show that \(P(1)\) is true.
Answer
\(P(1)\) is the proposition that \(\sum_{k=1}^1 (2k-1) = 1^2\), and that this holds true was shown in Question a. In fact, from Question a we know that \(P(n)\) holds true for \(n \in \{1,2,3,4,5\}\), but for the base case of the induction, checking the case where \(n=1\) is sufficient.
Question c#
Now carry out the induction step, and then use the induction principle to conclude that \(P(n)\) is true for all natural numbers \(n\).
Hint
In the induction step you must show that, for an arbitrary integer \(n \ge 2\), the implication \(P(n-1) \Rightarrow P(n)\) is true. In other words, for the induction step you may assume that \(P(n-1)\) is true (this is what we call the induction hypothesis), and then you must show that under this assumption, \(P(n)\) is also true.
Hint
In the induction step, the recursive definition of the summation symbol as given in Equation (3.5) in the textbook will be of use.
Exercise 3: A Geometric Series#
A geometric sequence is a sequence of numbers in which each number equals the previous number times a fixed factor. A geometric series is the sum of such a geometric sequence. Let us study such geometric series in this and the next exercises.
Let \(r \in \mathbb{C} \setminus \{1\}\) be a complex number and \(n\) a natural number. We wish to prove the following relation:
Question a#
Why can \(r\) not be equal to \(1\) in this identity?
Answer
If \(r=1\), then the denominator in the fraction \(\frac{r^{n+1}-1}{r-1}\) equals zero. Thus, the fraction is not defined for \(r=1\).
Question b#
Check that the identity holds true for \(n=1\).
Hint
If we consider the expression \(r^2-1\) as a polynomial in the variable \(r\), then we will find that it has the two roots \(1\) and \(-1\). Now, use Lemma 5.6.2 in the textbook to write \(r^2-1\) as a product of two linear (first-degree) polynomials.
Question c#
Show that the identity \(1+r+\cdots + r^n= \frac{r^{n+1}-1}{r-1}\) holds true for all natural numbers \(n\).
Hint
Use induction on \(n\). Note that the base case has already been handled in Question b.
Hint
For the induction step, the induction hypothesis is that \(1+r+\cdots + r^{n-1}= \frac{r^{n}-1}{r-1}\). Now use the fact that \(1+r+\cdots + r^{n}=(1+r+\cdots + r^{n-1})+r^n\), and then apply the induction hypothesis.
Exercise 4: A Bouncing Ball as a Geometric Series#
Question a#
A bouncing ball is released from a height of two meters above the floor. After hitting the floor, it bounces back up one meter, the second time half a meter, then a quarter of a meter at the third bounce, and so on. In other words, the falling distance is halved for each subsequent drop. Let \(n\) be a natural number. Provide an expression that produces the total distance the ball has traversed the moment it hits the floor the \(n\)-th time.
Hint
The first time the ball hits the floor, it has traversed through a total distance of two meters (because it was dropped from an initial height of two meters). The second time, the ball bounces one meter back up and then falls one meter back down again - in total the ball has now traversed \(2+2\cdot 1=4\) meters. The third time, it bounces back up half a meter before falling that half a meter back down again, so in total \(2+2\cdot (1+\frac12)\) meters. The fourth time we in a similar manner find the total traversed distance to be \(2+2\cdot (1+\frac12+\frac14)\) meters. Do you recognize a pattern and can you express it using the Sigma summation symbol?
Answer
If \(n=1\), the answer is \(2\) meters. For \(n \ge 2\), the answer is \(2+2\cdot \sum_{j=0}^{n-2} \frac{1}{2^j}.\)
Question b#
How many meters does the bouncing ball traverse through before finally finding rest on the floor?
Hint
By choosing \(r\) and \(n\) fittingly, you can simplify the expression using the relation that was proven in Exercise 3:
What do you get as \(n\) approaches infinity?
Answer
\(6\) meters.
Exercise 5: An Inequality#
A sequence of real numbers \(a_1,a_2,\dots\) is defined recursively as follows:
\(a_1=0\), and \(a_n=\sqrt{2+a_{n-1}}\) if \(n \ge 2\).
Question a#
Calculate \(a_1,a_2,a_3,\) and \(a_4\).
Answer
\(a_1=0\), \(a_2=\sqrt{2}\), \(a_3=\sqrt{2+\sqrt{2}}\), and \(a_4=\sqrt{2+\sqrt{2+\sqrt{2}}}.\)
Or in numerical versions with plenty of decimals:
\(a_1=0.00000000000000000000000000000\).
\(a_2=1.41421356237309504880168872421\).
\(a_3=1.84775906502257351225636637879\).
\(a_4=1.96157056080646089825236447227\).
Question b#
The claim is now that it for all natural numbers \(n\) is true that \(a_n<2\). Prove this using induction on \(n\).
Hint
For the induction step you may use the fact that the square-root function \(f: \mathbb{R}_{\ge 0} \to \mathbb{R}\) given by \(x\mapsto \sqrt{x}\) is strictly increasing.
Exercise 6: Area under a Parabola#
Let \(N\) be a positive real number and \(n\) a natural number. We define \(d=N/n\). As is most likely known from highschool, the area between the parabola and the first axis between \(x=0\) and \(x=N\) can be computed as a definite integral as follows:
In this exercise we wish to investigate how well this area is approximated using the finite sum \(\sum_{k=1}^n d\cdot(kd)^2\). The situation is illustrated in the following figure:
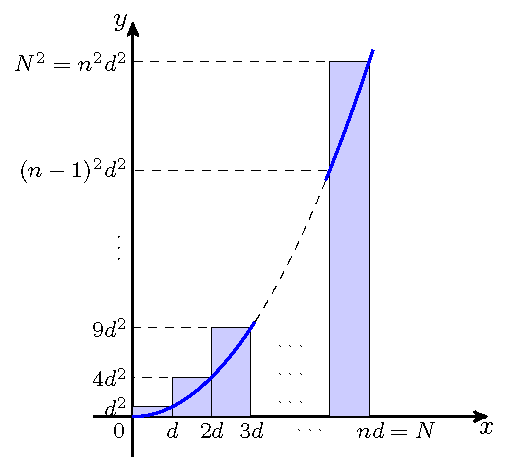
Question a#
Use the figure above to realize that
Question b#
The following distributive rule holds true for all natural numbers \(n\) and all complex numbers \(a,b_1,\dots,b_n\):
Use this fact to realize that
Question c#
Use induction on \(n\) to realize that \(\sum_{k=1}^n k^2=\frac13 n(n+1/2)(n+1)\) for all natural numbers \(n\).
Hint
In the induction step you will most likely at some point get to the formula
One could expand this expression by multiplying through and then check that it gives the correct result, but a lot of work can be saved by first factorizing \(n\) outside of the brackets:
Now, try first to realize that the expression within the brackets equals \(\frac13 (n+1/2)(n+1).\)
Answer
For the base case, if \(n=1\), the formula applies since \(\sum_{k=1}^1 k^2=1^2=1\) agrees with \(\frac13 1(1+1/2)(1+1)=\frac{3}{3}=1\).
For the induction step, if \(n \ge 2\), and if we assume the induction hypothesis which says that \(\sum_{k=1}^{n-1} k^2=\frac13 (n-1)(n-1/2)n\), we get
For example, by following the above hint it should be possible to realize that \(\frac13 (n-1)(n-1/2)n+n^2=\frac13 n(n+1/2)(n+1)\), which means that the induction step holds true. The induction principle hence implies that the formula \(\sum_{k=1}^n k^2=\frac13 n(n+1/2)(n+1)\) applies for all natural numbers \(n\).
Question d#
Now show that \(\sum_{k=1}^n d\cdot (kd)^2=\frac{1}{3}N(N+d/2)(N+d)\).
Answer
Based on the previous Questions we have
For the last equation sign, we used the fact that \(N=dn\).
Note that this equation implies that if \(N\) is held fixed while \(n\) goes towards infinity, then \(d\) goes towards zero, and the sum hence goes towards \(\frac13 N^3,\) which precisely is the area under the parabola.
